Mis mõjutab pooli induktiivsust?
Pooli induktiivsust mõjutavad järgmised tegurid:
- Keerdude arv (Vähem keerde = Väiksem induktiivsus, Rohkem keerde = suurem induktiivsus)
- Keerdude läbimõõt ja kuju (Väiksem diameeter = väiksem induktiivsus, Suurem diameeter = Suurem induktiivsus)
- Pooli pikkus (keerdude vahekaugus. Hõredamalt keerde = vähem induktiivsust, Tihedamalt keerde = Rohkem induktiivsust)
- Pooli südamiku magnetiline läbitavus (materjal), kuju, suurus. Õhksüdamiku magnetiline läbitavus (μ - permeability) on 1.
- Sagedus. Erinevad südamikumaterjalid "võimendavad" induktiivsust erinevatel sagedustel erinevalt
Kas on veel midagi, mida võiks induktiivpoolidest teada?
Ikka on. Kui me räägime induktiivsusest, siis skeemi seisukohalt pole induktiivsuse numbril suurt väärtust. Pigem huvitab meid selle pooli impedants Z töösagedusel. Impedantsi üks komponente on pooli induktiivtakistus XL, mis on tugevas sõltuvuses sagedusest.
Kuna pooli kerimiseks kasutatud traat omab ka (aktiiv) takisutst, siis võime induktiivpooli skemaatiliselt välja joonistada nii:

Impedantsi Z saame arvutada järgmise valemi abil:
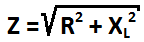
R – pooli aktiivtakistus (tavalise multimeetriga mõõdetav)
XL = Induktiivtakistus (Inductive reactance)
Impedantsi mõõtühikuks on oom, Ω (nagu ka tavalise takistuse puhul) ja seda väärtust saame kasutada ka meile ilmselt juba tuttava oomiseaduse valemites. Selle kohta leiad artikli lõpus ka pisikese näite.
0Hz sagedusel ehk alalisvoolu korral on meie pooli takistuseks kerimiseks kasutatud traadi takistus, mida saame lihtsalt mõõta tavalise multimeetriga. Vahelduvvoolu puhul aga hakkab seal poolis toimuma üks paras hookus-pookus, ning lisandub pooli induktiivtakistus, mis on otseses sõltuvuses sagedusest.
XL = 2 * Pi * f * L
Pi = 3,1416
f = Sagedus (Hz)
L = Pooli induktiivsus (H)
Nagu valmist näeme siis kasvatades sagedust, kasvatame ka induktiivtakistust XL.
Paneme nüüd valemi excelisse ja joonistame graafiku. Võtsin aluseks Vishay IMS-2 seeria aksiaalse induktori induktiivsusega 100μH (SRF = 10.5MHz, sealt tagasiarvutatuna saan tuletuslikuks mahtuvuseks ~2.3pF, DCR = 16.8Ohm)

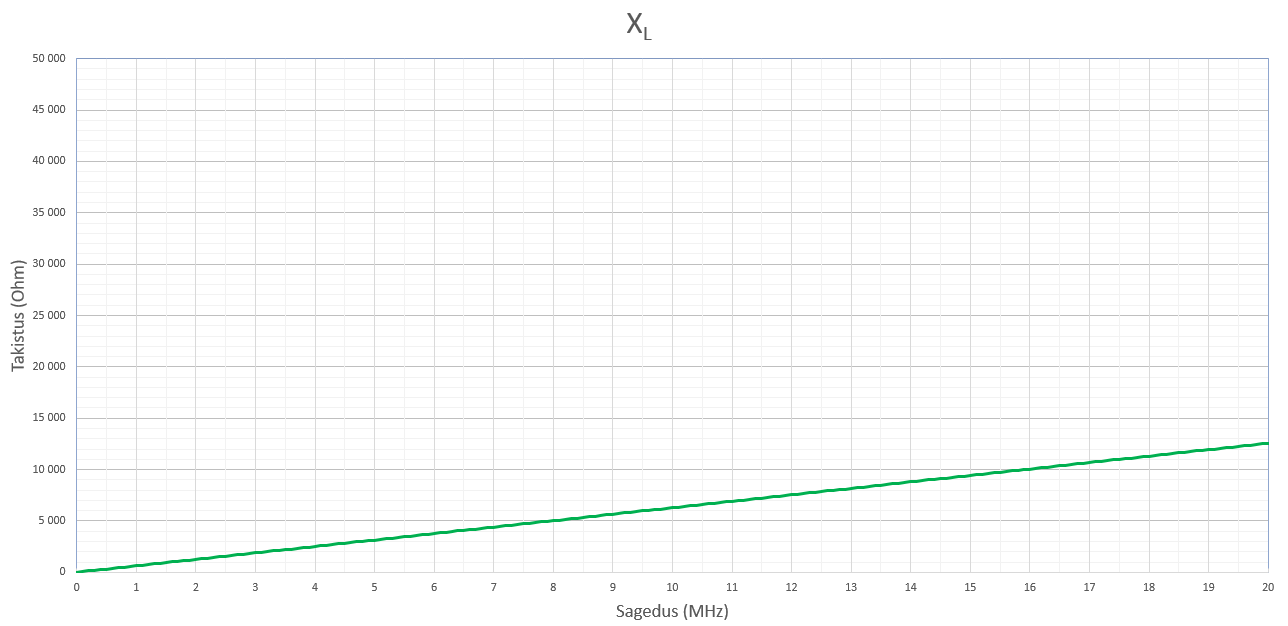
Graafiku roheline joon on pooli Induktiivtakistus (arvestamata aktiivtakistust R)
Nagu graafikult näha, on sageduse ja induktiivtakistuse suhe lineaarne ja sageduse muutumisel muutub meie pooli induktiivtakistus. 0MHz sagedusel on takistus praktiliselt null (pooli Z on võrdne pooli kerimiseks kasutatud traadi takistusega). 20MHz sagedusega vahelduvvoolule on aga takistus juba ca 13 kilo oomi. Päris suur muutus, kas pole?
Mis selle teadmisega peale hakata, kus seda kasutada? Lihtne näide. Induktiivpoole saab kasutada filtrite ehitamiseks. Kui ühendada piisava induktiivsusega pool tavalise kõlariga jadamisi, siis madalad sagedused (bassid) lähevad poolist pea takistuseta läbi, aga kõrgematel sagedustel pooli takistus kasvab ja need sagedused summutatakse. Loomulikult on hea filtri ehitamiseks vaja natuke rohkem komponente kui ainult üks pool, aga loodan, et antud näide andis natuke aimu ja aitab mõista, kuidas induktiivpool mõjutab meie skeemi.
Siiani rääkisime ideaalsest induktiivpoolist. Nagu teame, siis kahjuks ideaalseid asju ei eksisteeri. Kahjuks. Nii ei ole olemas ka ideaalset induktiivpooli ja me peame arvestama teatavate kõrvalnähtudega. Üheks olulisemaks on pooli keerdude vahel tekkiv mahtuvus ja nagu ülal juba mainitud, mängib rolli ka pooli kerimiseks kasutatud traadi takistus. Kõike seda teades ja arvesse võttes võime joonistada lihtsa pooli üles järgmise skeemina...
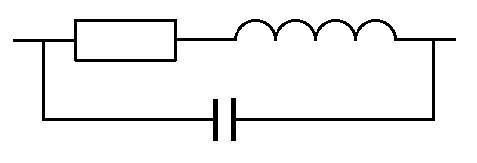
Nagu skeemilt näeme, tekib meil poolile paralleelne mahtuvus ja seda vastu meie enda tahtmist. See tähendab, et peame arvestama lisaks induktiivtakistusele ka mahtuvusliku takistusega. Paneme selle ka samale graafikule, kasutades samu lähteandmeid.
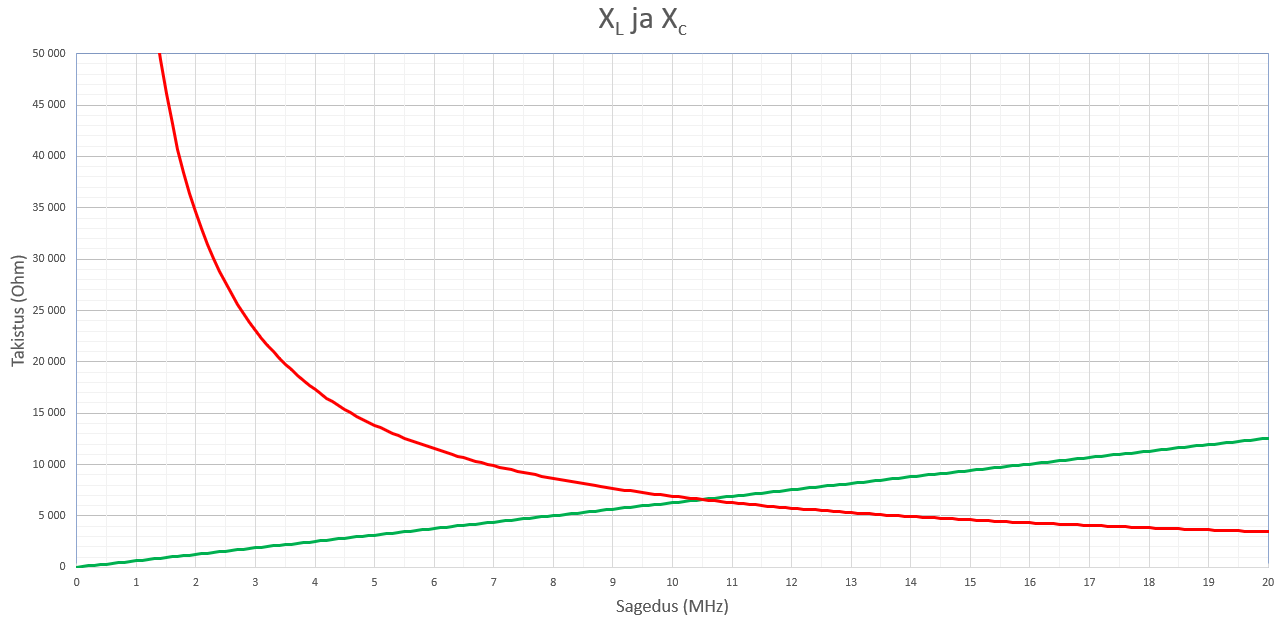
Graafiku roheline joon on pooli Induktiivtakistus (arvestamata aktiivtakistust R) ning punane on mahtuvuslik takistus
Nagu graafikult näeme, on antud induktiivpooli mahtuvuslik takistus madalatel sagedustel marginaalne ning see pooli üldist takistust allapoole ei tõmba. Võime tõmmata paralleeli takistite rööpühendusele. Kui ühendame paralleeli kaks takistit, milledest üks on üle 13k ja teine alla 13 oomi, siis selle 13k takisti olemasolu olulisel määral takistuste summat ei mõjuta. Kui liigume mööda graafikut edasi, näeme, et takistuse kõverad ristuvad (nii induktiiv kui ka mahtuvuslik takistus on võrdsed) ja mööduvad teineteisest. Selles regioonis on olukord juba teine ja me peame kindlasti arvestama pooli mahtuvusliku komponendiga.
Mis aga juhtub meie pooli impedantsiga? Impedantsi saame arvutada järgmiselt:
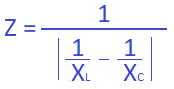
Kasutame jälle Exceli abi ja joonistame uue värvilise pildi lisaks, kasutades ikka samu lähteandmeid, mis ülal aluseks võtsime.
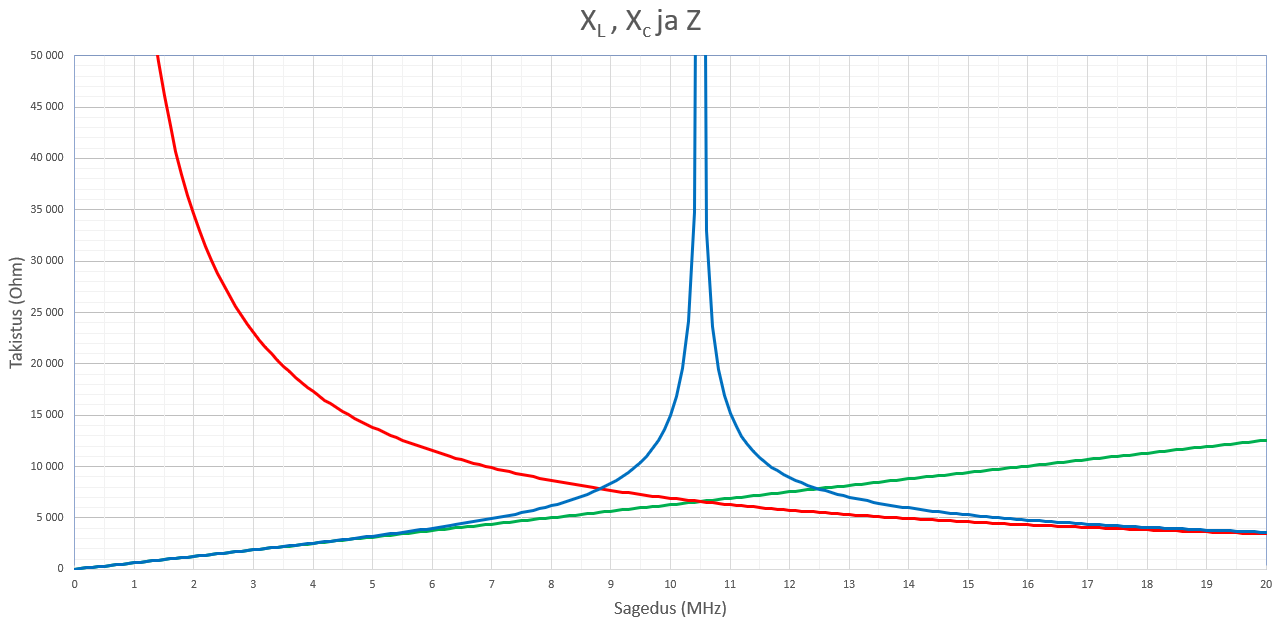
Graafiku roheline joon on pooli Induktiivtakistus (arvestamata aktiivtakistust R), punane on mahtuvuslik takistus ja sinine on tegelik takistus Z
Antud 100uH induktiivsus toimib ettearvatavalt kuni 6MHz sageduseni. Edasi hakkab pooli induktiivtakistus järsult kasvama. Punktis, kus Xl ja Xc lõikuvad, sööstab pooli tegelik takistus Z raketina taevasse. Seda punkti nimetatakse pooli oma resonantssageduseks (SRF – Self Resonant Frequency). Sagedus, kus induktiivpool resoneerub ise enda mahtuvusega. Teadupärast LC paralleel võnkeringi takistus resonantssagedusel on lõpmatus.
Selle punkti ületamisel muutub pool mahtuvuslikuks. Ehk töötab pigem nagu kondensaator. Sageduse kasvades hakkab takistus langema, mitte vastupidi nagu võiks induktiivpoolilt oodata. Seda põhjusel, et pooli mahtuvuse osatähtsus hakkab ületama induktiivsuse osakaalu.
Mida see meile tähendab? Toome näite. Hakkame ehitama ribafiltrit (BPF – band pass filter). Teostame mõne programmiga arvutused, soetame soovitud nominaalidega komponendid. Peale filtri valmimist selle karakteristikut mõõtes selgub, et läbilaske riba ei paikne päris seal, kuhu me selle projekteerisime. Seda sellepärast, et kalkulaatorid arvestavad ideaalsete induktiivpoolide ja kondensaatoritega ega võta arvesse parasiitkomponente (mõned kalkulaatorid võimaldavad arvesse võta ka mahtuvuse või induktiivsuse reaalse mudeli) .
Enne skeemi kokku panemist mõõtsin komponendid üle ja kõik olid õige. Kas programm arvutas valesti? Ei. Kuigi meie poolide induktiivsused ja kondensaatorite mahtuvused olid mõõtmisel sellised nagu peaks, ei mõõtnud me komponendi induktiivsust (induktiivtakistust) valitud töösagedusel.
Leidsin skeemi, kus olid filtri komponentide väärtused näidatud ja ka mõõtetulemused olid olemas. Miks minu ehitatud filtri graafik erineb skeemi autori omast? Selleks, et korrata kellegi skeemi, tuleb kasutada sama tootja sama tüüpi komponente. Nii kondensaatoreid kui ka induktiivsusi. Seda isegi siis, kui valite uued komponendid nii, et jääte kaugele SRF punktist, n.ö lineaarsele osale. Võib ju olla, et skeemi autor ei olnud nii hoolikas, aga filtri häälestamisel kompenseeris kõrvalnähud.
Soovitus: Kui ehitate filtreid või võnkeringe, siis valige pool nii, et omaresonantssagedus (SRF) oleks ca 10x kõrgemal projekteeritud maksimaalsest sagedusest. Kui aga tegemist on signaali summutava ahelaga (näiteks pool RF võimendi transistori toiteahelas, mis peab takistamas kõrgsagedus signaali liikumist toiteliinile), võib pooli valida omaresonantssageduse lähedale. Nii on selle takistus kõrgsagedussignaalile võimalikult kõrge, aga samas alalisvoolule on takistuseks ainult pooli traadi takistus.
!!! Mida suurem on pooli induktiivsus, seda suurem on tõenäoliselt ka pooli parasiitmahtuvus ja sellest tulenevalt ka madalam omaresonants sagedus (SRF).
!!! Kui kasutate standardkomponente, saate vaadata tootja kataloogist valitud komponendi omaresonantssageduse ning selle abil arvutada pooli parasiitmahtuvuse. Seda teades saate filtri projekteerimisel sellega juba arvestada.
Kui kerite pooli ferriit või rauapurust südamikule, peate ka arvestama, et südamiku mõju induktiivsusele (AL väärtus) on erinevatel sagedustel erinev (sõltub kasutatavast materjalist). Selletõttu võib pooli tegelik induktiivsus töösagedusel tublisti erineda arvutuslikust või mõõdetud induktiivsusest. Ideaalis tuleks keritud pooli induktiivsust mõõta töösagedusel, aga sellised aparaadid on õnnetuseks kole kallid. Lihtsamad induktiivsuse mõõtjad kasutavad 1kHz sagedust. Natuke parematel aparaatidel saab juba valida erinevate sageduste vahel (näiteks 100, 120Hz, 1, 10, 100kHz jne..)
Teeme ka väikese näite ja arvutame meie kasutatud induktiivsuse eeldatava parasiitmahtuvuse.
Komponent: Vishay IMS-2 induktiivpool
Induktiivsus: 100uH
Resonantssagedus: 10.5MHz
Neid andmeid teades, saame arvutada resonantsahela (võnkeringi) puuduva komponendi – mahtuvuse C.
LC ahela resonantssageduse saab arvutada järgmisest valemist:
f = 1 / (2 * Pi * SQRT(L * C))
Sellest valemi peame nüüd tagurpidi keerama, et leida sealt mahtuvus C. Valem näeb siis välja selline:
C = 1 / (4 * f2 * Pi2 * L)
Paneme numbrid valemisse ja saame teada, et meie pooli parasiitmahtuvus on 2,298pF. Seda teades saame filtrit modelleerides sellega juba arvestada.
Kui palju see mõjutab? Sõltub skeemist ja sagedustest. Alati on mõistlik seda ette kontrollida, kui tagantjärele tõdeda, et: „Ei tulnud päris nii nagu plaanisin.“
Kui induktiivsus pole nii väga oluline ja pigem on tähtis pooli takistus teatud sagedustel, siis milleks üldse induktiivsusest räägitakse? Kui me hakkaks markeerima poole stiilis „100 oomi/5MHz juures“, siis peame kogu karakteristiku välja kirjutama, aga ma kipun arvama, et komponendil pole nii pika jutu tarvis ruumi. Samuti oleks komponenti ostes seda oluliselt tülikam valida.
Kui valem on XL = 2 * Pi * f * L ja tegelik XL erineb arvutuslikust, aga f on meil teada ning see ei muutu, siis mis muudab arvutuse tulemust? Jääb järele ju ainult induktiivsus! Valem räägib ideaalsest poolist. Seda meil aga ei eksisteeri. Seega peame valemis lisaks L’ ile arvestama ka R ja C komponendiga. Kuniks nende komponentide osakaal on marginaalne, võime need jätta arvestamata, aga teatud sagedustel hakkavad need mängima olulist rolli ja me ei tohi neid enam eirata.
Kasutame taaskord exceli abi ja joonistame veel ühe värvilise pildi. Unustame ära teadmised parasiit mahtuvusest ja naaseme algse valemi juurde. Võtame aluseks, et kuidagi oleme saanud teada pooli induktiivtakistuse (XL) ja lähtuvalt sellest teeme tagasiarvutuse induktiivsusele. Tulemus näeb välja selline ...
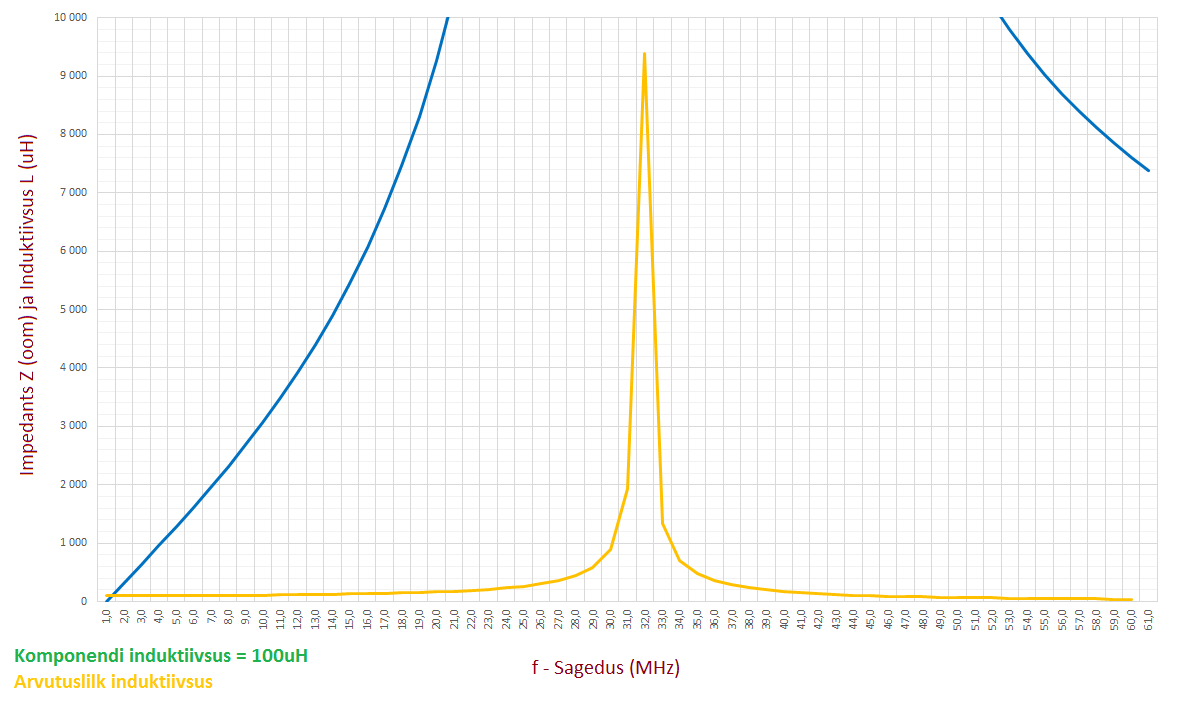
Pildil olev sinine joon on pooli impedants (induktiivtakistus XL + aktiivtakistus R) ja kollane on arvutuslik induktiivsus. Tõepoolest, nagu graafikult näha, siis sageduse kasvades kasvab ka induktiivsus ja see saavutab oma maksimaalse väärtuse koos maksimaalse impedantsiga. Võibolla olete googeldades leidnud ka teistmoodi graafikuid, mis ei sarnane minu joonistatud pildile, vaid näevad välja sellised...
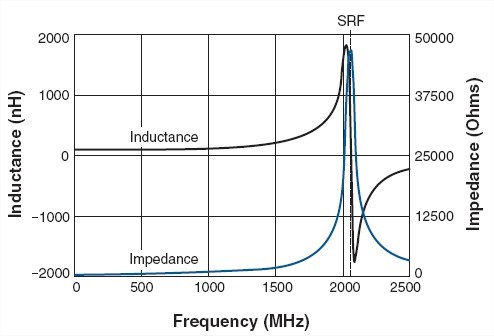
Ka siin pildil on kõik õige aga pange tähele, et induktiivsuse vahemik on vasakul vertikaalteljel -2000 kuni +2000. Kuna induktiivsus ei saa olla negatiivne, tuleb arvutustes võtta arvesse absoluutväärtus (excelis kasuta valemis =ABS(...) ). Minu joonistatud pildil on see just nii tehtud. Sellest ka visuaalne erinevus ühesugustel graafikutel.
Kuidas siis ikkagi on? Kui me mõõdame aparaatidega pooli takistust mingil kindlal sagedusel ja teeme sellest tagurpidi arvutusega induktiivsuse, siis tõepoolest võib tunduda, et sagedus mõjutab induktiivsust. Tegelikult me aga eirame fakti pooli parasiitmahtuvusest. Skeemi seisukohalt on meile oluline pooli induktiivtakistus projekteeritud sagedusel ja induktiivsuse number on lihtsalt üks number. Oluline on teada, mis pooliga erinevatel sagedustel toimub ning nende muutustega arvestada.
Kas pooli südamik ka pooli induktiivsust mõjutab? Erinevate südamike abil saame mõjutada pooli induktiivsust. Võtame näiteks Amidon T50-3 toroidsüdamiku. Üks keerd ümber T50 mõõdus toroidi on traadi pikkuses ~14,7mm. Õhksüdamikuga poolil teeks see keeru diameetriks 4,68mm. Võtame aluseks 20 keerdu (0.5mm traadiga) ja arvutame pooli induktiivsuse (kasutan vastavat kalkulaatorit ja saan tulemuseks 0,716uH. Arvutame nüüd T50-3 südamikul 20 keeruga pooli induktiivsuse ja saame vastuseks 7,00uH.
Südamik mõjub pooli induktiivsusele nagu võimendi. Erinevad südamikud võimendaad erinevalt. Selle koefitsendi leiab andmelehel realt või tulbast, mis kasutab tähiseks nimetust AL. Mainitud T50-3 pooli AL väärtus on 17.5. Induktiivsuse mikrohenrides saame järgmise valemi abil: L = (AL x T2) / 1000
L = Induktiivsus (uH)
AL = Induktiivsuse faktor
T = Keerdude arv
Erinevate südamike juures tuleb aga silmas pidada, millises sagedusvahemikus kasutamiseks need mõeldud on. Ülal näites kasutatud T50-3 toimib kõige paremini sagedusvahemikus 20kHz - 1MHz. See tähendab, et selles vahemikus on AL väärtus enam-vähem stabiilne ja deklareeritud suuruses. Sageduse kasvades hakkab südamiku võime induktiivsust võimendada vähenema, kuniks lõpuks pole enam vahet, kas meil on pool keritud südamikule või mitte.
Miks südamikke kasutada, kui need asja veel keerulisemaks ajavad? Südamikud aitavad oluliselt vähendada keerdude arvu soovitud induktiivsuse saavutamiseks. Vähem keerde tähendab vähem traati ja see omakorda väiksemat aktiivtakistust. Väiksem traadi takistus annab meile parema Q (pooli kvaliteedi faktor).
Q = 2 x Pi x f x L / R
Pi - 3,14
f - Sagedus (Hz)
L - Induktiivsus (H)
R - Aktiivtakistus (Oom)
Valemist näeme, et mida väikesm on R, seda suurem on Q
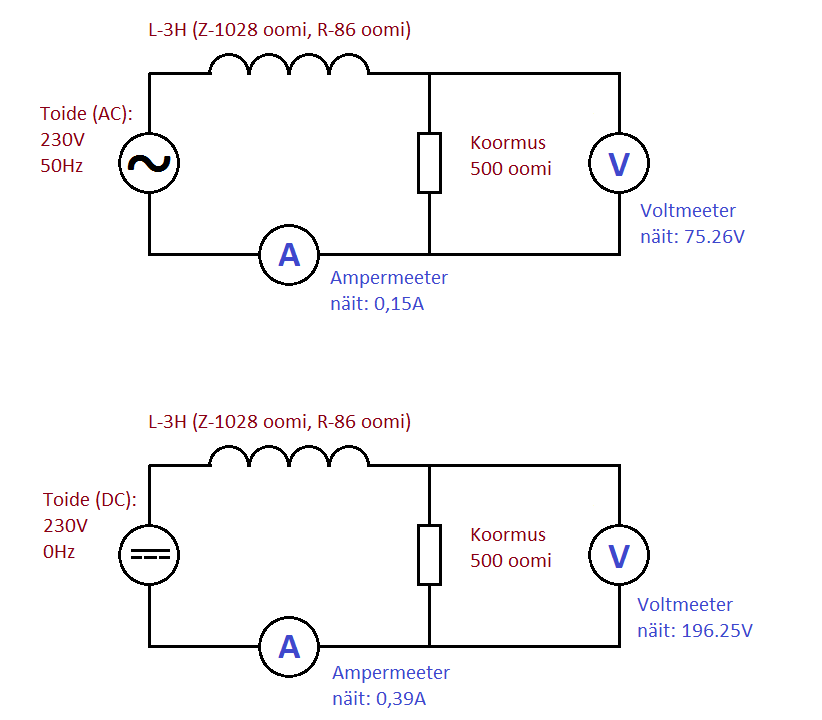
Nagu ülalpool lubatud, toome ka lihtsa näite, mis illustreerib induktiivpooli mõju erinevatel sagedustel. Võtame aluseks seinakontaktist leitava 50Hz sagedusega vahelduvvoolu.
Skeem on lihtne pingejagur. Mõlemas skeemis on kõik komponendid samade nominaalidega. Samaks jääb ka toitepinge. Ainus, mida muudame on toitepinge sagedus. Esimesel skeemil toidame vooluringi 230V vahelduvvooluga ja teisel skeemil alalisvooluga. Usun, et pikemaid kommentaare pole vaja anda ja põhjused, miks on sellised erinevused voltmeetri ja ampermeetri näitudes oskate nüüd juba ise välja mõelda.