Ilmselt te teate, mis on takisti ja mis on takistus. Eeldatavasti olete kursis ka Ohmi seadusega. Kui olete sellest kord aru saanud, on see lihtne ja arusaadav ning ei lähe enam meelest, nagu jalgrattaga sõitmine.
Kas teadsite, et ka kondensaatoril ja poolil on takistus? On. Aga kui suur on see takistus? Lihtne, mõõdame multimeetriga?! Me näeme, et kondekas on 'katki', takistus on lõpmatu ja pooli takistus on nullilähedane (lühis). Aparaat ei valeta ja nii see on.
Aga seda ainult alalisvoolu (DC) puhul. Vahelduvvoolule (AC) võib kondensaatori takistus olla ka alla oomi ja pooli takistus seevastu üle megaoomi.
Kuidas nii? Sellest arusaamiseks piisab, kui teate, et vahelduvvoolu oluline parameeter on sagedus (f), mis omakorda mõjutab oluliselt kondensaatori ja pooli takistust. Mida kõrgem on sagedus, seda väiksemaks muutub kondensaatori takistus. Induktiivpoolil toimib see täpselt vastupidi. Sageduse kasvades kasvab ka takistus.
Kuidas seda arvutada? Induktiivtaksitust tähistatakse tähisega XL (inductance) ning mahtuvuslikku takistust tähisega XC (capacitance). Vastuse saame takistusena Ohmides. Arvutamiseks kasutame järgmiseid valemeid.
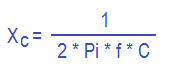

XC - Mahtuvuslik takistus (Ohm)
XL - Induktiivtakistus (Ohm)
Pi - 3,14
f - Sagedus (Hz) [ärge unustage ühikuid teisendada]
C - Mahtuvus (F) [ärge unustage ühikuid teisendada]
L - Induktiivsus (H) [ärge unustage ühikuid teisendada]
Teeme näiteks mõned arvutused 10nF kondensaatoriga erinevatel sagedustel:
C = 10nF
f1=1kHz, f2=1MHz, f3=100MHz
Xc @ f1 = 1 / ( 2 x 3.14 x 1 000 x 0.00000001) = 15 923 Ohm (15,9 kOhm)
Xc @ f2 = 1 / ( 2 x 3.14 x 1 000 000 x 0.00000001) = 15,92 Ohm
Xc @ f3 = 1 / ( 2 x 3.14 x 100 000 000 x 0.00000001) = 0,16 Ohm
Eelnevalt me juba teame, et alalisvoolu (DC) puhul on kondensaatori takistus lõpmatu (ideaalse kondensaatori puhul, reaalselt sõltub see kondensaatoris kasutatavast isolaatori materjalist). Arvutustest näeme, et sageduse kasvades taksitus väheneb. Mida suurem on sagedus, seda väiksemaks muutub takistus. Tänu sellele efektile saame kasutada kondensaatoreid erinevate sõlmede alalisvoolu ahelate eraldamiseks teineteisest, samas vahelduvvoolu signaal (audio või raadio sagedused) lipsab läbi kondensaatori rõõmsalt ühest astmest teise. Või siis vastupidi, alalisvoolu ahelates soovimatute häirete (vahelduvvoolu signaalide) eemaldamiseks, ühendades toiteahela + ja - vahele kondensaatori.
Aga ka siin peame tõdema, et antud valemi puhul on tegemist ainult teooriaga, mis kehtib ideaalse kondensaatori puhul. Reaalses elus hakkab meid segama kondensaatori enda induktiivsus. Loe sellest lähemalt SIIT.
Arvutame nüüd ka 1nH induktiivpooli takistuse samadel sagedustel:
L = 1nH
f1=1kHz, f2=1MHz, f3=100MHz
XL @ f1 = 2 x 3.14 x 1 000 x 0.001 = 6,28 Ohm
XL @ f2 = 2 x 3.14 x 1 000 000 x 0.001 = 6 280 Ohm (6,28 kOhm)
XL @ f3 = 2 x 3.14 x 1 000 000 000 x 0.001 = 6 280 000 Ohm (6,28 MOhm)
Kui alalisvoolule on pooli takistuseks ainult mähise traadi takistus (sama induktiivsuse juures võib olla mähise traadi takistus erinev. See sõltub mähise traadi ristlõike pindalast ja traadi pikkusest. Erinevad pooli südamikud nõuavad sama induktiivsuse saavutamiseks erineva arvu keerde), siis arvutustest näeme, et sageduse kasvades kasvab ka takistus. Nii saame kasutada induktiivpoole näiteks vahelduvvoolu ahelate eraldamiseks alalisvoolu ahelatest. Kindlasti olete märganud selliseid skeemi lahendusi....
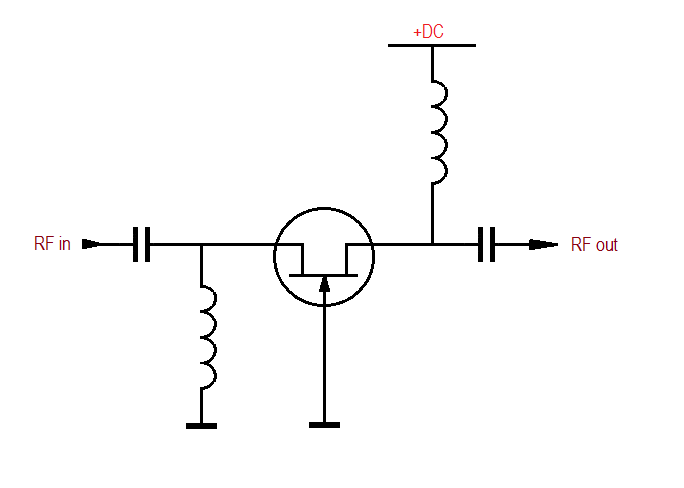
... ja imestate, et kuidas see üldse töötab. Testriga mõõtes on ju pooli takisus olematu. Võimendi sisend on ühendatud üle krussis traadijupi vastu maad ja väljund vastupidi otse toitele. Kas skeemi koostaja oli üldse kaine, kui ta selle joonistas? Nüüd me teame, et oli. Kõik on korrektne ja skeemi joonistaja teadis täpselt mida tegi. :)
Paneme nüüd oma teadmised XL ja XC kohta kokku ja vaatame järgmisi skeeme...
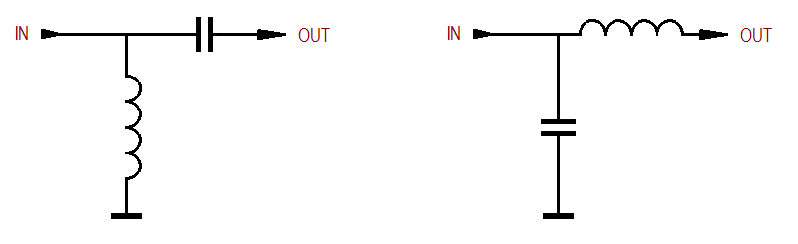
... üks piltidest on madalpääsfilter (LPF - low pass filter) ja teine kõrgpääsfilter (HPF - high pass filter). Kumb on kumb? Kumb skeem laseb läbi madalad sagedused ja takistab kõrgematel läbipääsu ja kumb vastupidi? Vastuse mõtlete juba ise välja :)